SAFE

Imputation of missing data

The problem of data availability is crucial, although it is common in sustainability studies (see, e.g., Esty et al., 2005). SAFE needs 75 basic indicators per country as inputs to assess all aspects of sustainability. For the 128 countries considered, a total of 128×75= 9,600 normalized inputs are required. However, because only few counties provide data for all indicators, 284 values (approximately 3% of the data) are missing. To ameliorate this situation a data imputation procedure is performed.

As a first step of the imputation procedure, countries are grouped by similarity according to geographic, economic, and cultural criteria. This is done as follows:

  1. Country groups are formed according to geography as given by the United Nations Statistics Division (2010)
  2. These groups are refined, taking into account economic criteria. Such country groupings are also given by the United Nations Statistics Division (2010) and the World Bank (2010). For example:
    1. The group of Baltic countries is separated from the group of Scandinavian countries, since the latter forms a group of high-income OECD countries, although they all belong to the geographic area of North Europe.
    2. UK and Ireland are grouped together with other Western European countries, although they are located in North Europe in order to form a homogenous group of OECD countries and high-income developed economies.

The resulting groups consist of highly similar countries (sij = 2), as shown by the rectangular boxes of Fig. 5.

  1. Pairs of groups with moderate similarity are found using geographical and economic criteria. For example:
    1. Western European countries are moderately similar to other OECD members which belong to the groups of North America, Scandinavia, South Europe, and Japan.
    2. The group of South America consists of middle-income countries which are moderately similar to Central American countries, but not to the high-income OECD countries in North America.

The result of this step is presented by the arrows of Fig. 5, which correspond to moderately similar (groups of) countries (sij = 1).

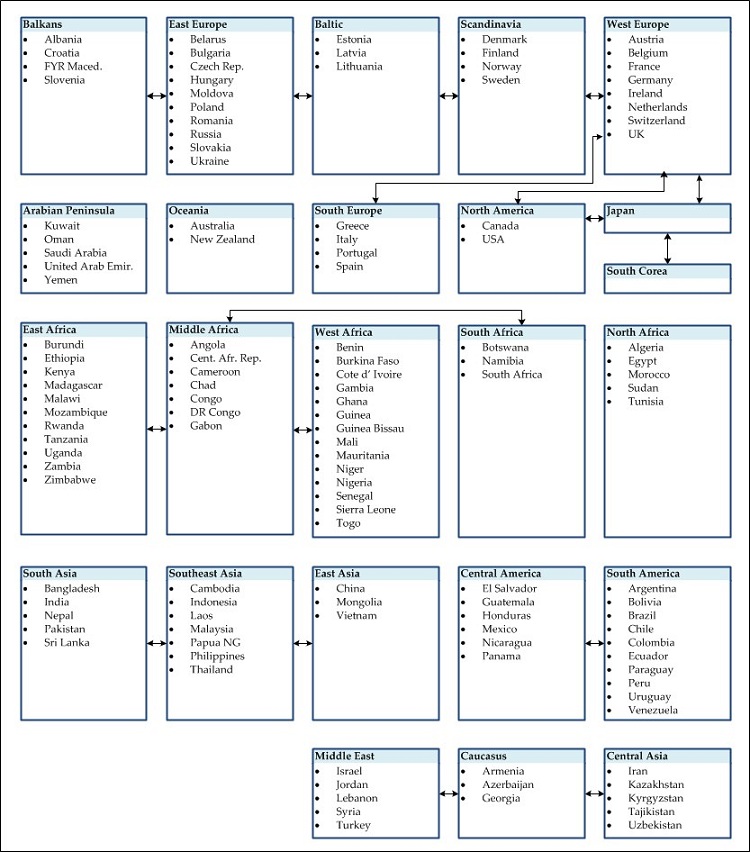
Countries with high similarity (boxes) and moderate similarity (arrows).
Fig. 5. Countries with high similarity (boxes) and moderate similarity (arrows).

In the second step of the imputation procedure a distance matrix is set up that measures how different are the available data of a country from those of another similar country. The basic indicators fall within 8 groups:

  1. LAND,
  2. WATER,
  3. BIOD,
  4. AIR,
  5. POLICY,
  6. WEALTH,
  7. HEALTH, and
  8. KNOW.

Suppose that some basic input from indicator group g is not available for country i. Let j be an index of countries similar to i, i.e., sij = 1 or 2. For each pair (i, j), the Euclidean distance dijg is computed using those normalized indicators of group g for which data are available for both i and j. The Euclidean distance is given by the square root of the average of squared indicator differences:

\[{{\rm{d}}_{{\rm{ijg}}}}{\rm{ = }}\sqrt {\frac{{\sum\limits_{\scriptstyle{\rm{available }}\;{\rm{indicators }}\atop\scriptstyle{\rm{c }}\;{\rm{of}}\;{\rm{ group}}\;{\rm{ g }}} {{{\left( {{{\rm{x}}_{{\rm{ic}}}}{\rm{ - }}{{\rm{x}}_{{\rm{jc}}}}} \right)}^{\rm{2}}}} }}{{{\rm{number }}\;{\rm{of }}\;{\rm{group }}\;{\rm{g }}\;{\rm{indicators }}\;{\rm{available }}\;{\rm{for }}\;{\rm{both }}\;{\rm{i }}\;{\rm{and }}\;{\rm{j}}}}} \]

where xic is the normalized value of indicator c for country i, which is obtained by exponential smoothing (step 2 of Fig. 1). When no group g indicator is available for both countries i and j the corresponding Euclidean distance is assumed to be infinite, i.e., \({d_{ijg}} = \infty \) .

In the third and last step of the imputation procedure the missing value of an indicator is filled in using the average value of this indicator over all countries with maximum similarity and minimum Euclidean distance. Suppose that an indicator of group g is not available for country i. The following algorithm is used to find countries that meet the similarity and distance criteria. Index j runs exclusively over those countries for which the indicator to be imputed is available.

  1. Compute dijg for each country j in the same group as i (sij = 2). Find those countries for which dijg ≤ 0.1 (10% of the maximum value of a normalized indicator). If no countries are found, then go to step 2.
  2. Compute dijg for all moderately similar countries (sij = 1). Choose those countries for which dijg ≤ 0.1. If no country satisfies this, then go to step 3.
  3. Find countries in the same group as i (sij = 2) for which dijg ≤ 0.2 (20% of the maximum value of a normalized indicator). If no countries are found, then go to step 4.
  4. Find moderately similar countries (sij = 1) for which dijg ≤ 0.2. If no countries are found, then go to step 5.
  5. Compute dijg for each unrelated country j (sij = 0) and select those with the minimum distance.

Using the above algorithm, a complete data base is formed for 128 countries and 75 indicators per country. On average, 1.86 or about two countries are chosen to impute each of the 284 missing inputs. The average value of distances dijg is 0.105, with an average range of 0.012.

References